

 Пример 1 - эпюры ВСФ для балки
Пример 1 - эпюры ВСФ для балки
(рис 4 - рис 7)
- Обозначаем возможные реакции опор: (для шарнирно-подвижной опоры: 1 реакция (в этом примере - YB)), для шарнирно-неподвижной: 2 реакции (YA и ZA). (Так как заданная нагрузка не имеет составляющих, параллельных оси Z, то ZA=0). Для опоры-защемления (заделки) в плоской задаче возможны 3 реакции (2 компоненты вдоль координатных осей и пара сил (реактивный момент)). В примере такой опоры нет.
- Так как балка неподвижна, система приложенных к ней внешних сил (включая опорные реакции) уравновешена. Так как задача плоская, то можно составить 3 независимых уравнения статики для определения неизвестных реакций опор. Так как неизвестных 3, это возможно.
- Однако проблема в том, чтобы из бесчисленного множества уравнений, которые вообще можно составить, записать только выгодные нам уравнения: желательно, чтобы в каждое уравнение входило одно неизвестное. Здесь это возможно. Используем так называемые моментные точки A и B
- Составим и решим уравнения (см рис 7).
Подробнее об определении реакций написано здесь. Перед составлением уравнений опоры (строго говоря) нужно мысленно отбросить, заменив их воздействия на балку статическим экавивалентом - опорными реакциями YA, YB, ZA(неизвестными). При составлениии уравнений статического равновесия естественно применять правила знаков статики, т е: пара сил, действующая против часовой стрелки, считается положительной, проекция силы на ось, направленная в ту же сторону, что и ось - тоже положительна.
4-е уравнение необходимо составить для проверки, так как все мы можем ошибаться.
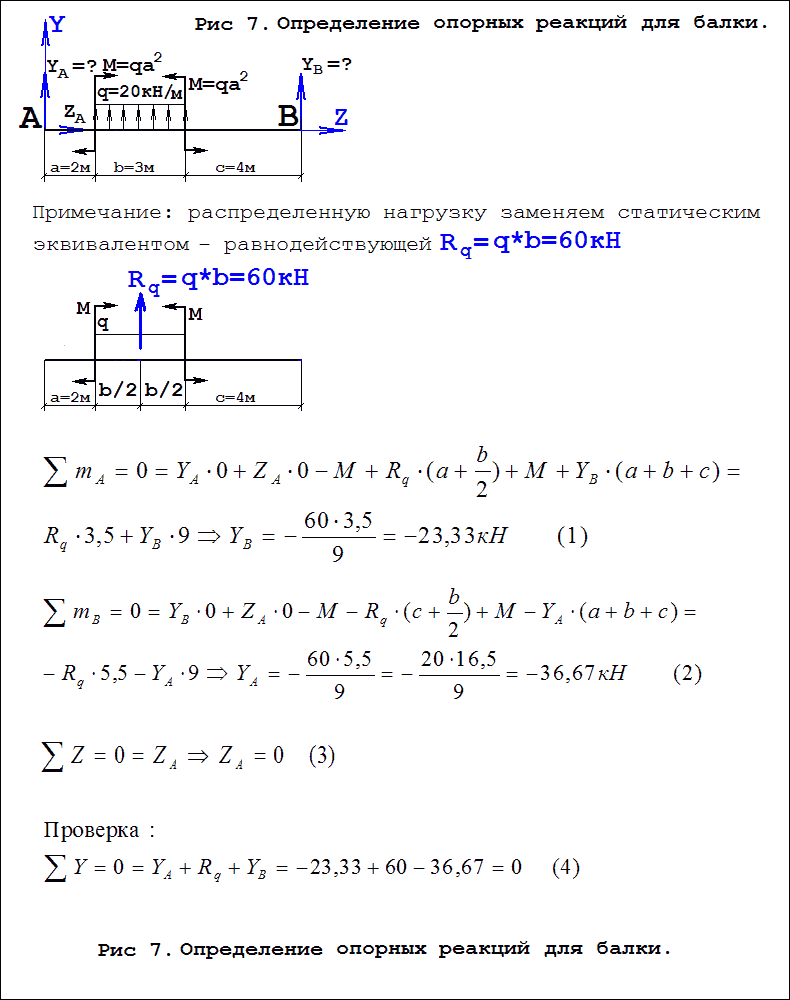

Для определения величины ВСФ применяется метод сечений. Последовательность действий при построении эпюр показана на рис 6.
- У реакций, получившихся со знаком минус удобно поменять первоначальное направление на противоположное. Можно не менять, но не забывать про минус. Реакции равные нулю - убрать.
- Разбить балку на ГРУЗОВЫЕ УЧАСТКИ. (см рис 6, участки 1,2,3).
- В произвольном месте каждого участка мысленно провести сечение, обозначить его на расчетной схеме (я обозначаю волнистой линией).
- Для каждого такого сечения выбрать из соображений удобства начало координат для отсчета продольной координаты Z сечения. Обычно началом координат выбирают начало или конец бруса или начало/конец какого-либо (обычно этого же) грузового участка. Не бывает "неправильного" начала координат, но очень часто бывают ошибки в определении координаты z сечения. Я выбирал так, чтобы обеспечить разнообразие.
- Обозначить координаты сечений: z1, z2, z3 и т д. Я обозначаю координату так: сечение, где находится начало координат - жирной черточкой. От нее веду линию со стрелкой к сечению, координату которого определяю (см рис 6).
- Задать пределы изменения каждой координаты (z1, z2, z3) из условия, что изменяя координату в этих пределах Вы изменяете положение сечения от одного края участка до другого.
Тогда получим: 0 < z1 < 2м; 2м < z2 < 5м;
0 < z3 < 4м;

- Определяем ВСФ в пределах 1-го участка (рис 6, 8).
- Сечение с координатой z1 (рис 6) разбивает балку на 2 части - левую и правую. ВСФ можно определять из уравнений равновесия любой (по выбору) из этих частей. Рекомендуется выбирать ту часть, рассматривать которую проще. Так как рассматривать одну нагрузку - YA проще чем четыре нагрузки, рассмотрим равновесие левой (от сечения) части балки (рис 8).
- Через т. С (центр тяжести поперечного сечения) проведены оси: Y, Z. Ось X не видна, так как перпендикулярна плоскости рисунка. Справа от сечения показаны возможные в плоской задаче внутренние силовые факторы: N - продольная сила, Q - поперечная сила, M - изгибающий момент. Рекомендуется предполагать их положительными. Так как отсеченная левая часть балки фактически неподвижна, то система приложенных к ней извне сил (YA, N, Q, M) уравновешена, поэтому можно записать любое уравнеине равновесия и оно будет выполняться, т е из него можно находить неизвестные ВСФ (N, Q, M). Эти уравнения представлены на рис 8. Напомню, что рекомендуются уравнения, в каждом из которых только одно неизвестное. Так как внешняя нагрузка проецируется на ось Z в нуль, продольная сила равна нулю (5) и на других участках определять ее не будем.
- Для построения эпюр вычислим ВСФ на границах 1-го участка, подставив в (6), (7) крайние значения z1, т е 0 и 2м. Получим (8), (9).
- Крайние точки для графика получены. Чтобы провести линии, нужно определить тип этих линий по ф. (6) и (7). Видим, что Q(z1) = Const, поэтому на эпюре Q проводим прямую, параллельную оси Z от левого значения Q=-36,67 до правого значения Q=-36,67.
Формула (7) показывает, что изгибающий момент M зависит ЛИНЕЙНО от z1, поэтому проводим наклонную прямую между точками (0; 0) и (2; -73,34).
( Механики откладывают отрицательные ординаты на эпюре моментов вниз, а строители - вверх. Эпюры на рис 6 построены для механиков.)
Программа МКЕ строит эпюры для строителей и для механиков, однако изучить работу с программой не намного легче, чем научиться строить эпюры самому.

- Сечение с координатой z1 (рис 6) разбивает балку на 2 части - левую и правую. ВСФ можно определять из уравнений равновесия любой (по выбору) из этих частей. Рекомендуется выбирать ту часть, рассматривать которую проще. Так как рассматривать одну нагрузку - YA проще чем четыре нагрузки, рассмотрим равновесие левой (от сечения) части балки (рис 8).
- Определяем ВСФ в пределах 2-го участка (рис 6, 9).
- Сечение с координатой z2 (рис 6) разбивает балку на 2 части - левую и правую. ВСФ можно определять из уравнений равновесия любой (по выбору) из этих частей. Рекомендуется выбирать ту часть, рассматривать которую проще. Здесь справа и слева по 3 нагрузки, поэтому рассмотрим равновесие левой (от сечения) части балки (рис 9).
- Через т. С (центр тяжести поперечного сечения) проведены оси координат. Справа от сечения показаны возможные в плоской задаче внутренние силовые факторы (в положительном направлении). Уравнения равновесия представлены на рис 9.
- Для построения эпюр вычислим ВСФ на границах 2-го участка, подставив в (10), (11) крайние значения z2, т е 2м и 5м. Получим (12) - (15).
- Крайние точки для графика получены. Чтобы провести линии, нужно определить тип этих линий по ф. (10) и (11). Видим, что Q зависит от z2 линейно, а M - квадратично, поэтому на эпюре Q проводим наклонную прямую, а на эпюре M - параболу - между крайними точками. Эпюра Q пересекает ось Z, значит, в этом сечении M экстремально (см (4) в начале: Q=dM/dz).
Для определения координаты экстремума пользуемся формулой (17 - рис 6), которую легко доказать.
( Механики откладывают отрицательные ординаты на эпюре моментов вниз, а строители - вверх. Эпюры на рис 6 построены для механиков.)

- Сечение с координатой z2 (рис 6) разбивает балку на 2 части - левую и правую. ВСФ можно определять из уравнений равновесия любой (по выбору) из этих частей. Рекомендуется выбирать ту часть, рассматривать которую проще. Здесь справа и слева по 3 нагрузки, поэтому рассмотрим равновесие левой (от сечения) части балки (рис 9).
- Определяем ВСФ в пределах 3-го участка (рис 6, 10).
- Сечение с координатой z3 (рис 6) разбивает балку на 2 части - левую и правую. ВСФ можно определять из уравнений равновесия любой (по выбору) из этих частей. Рекомендуется выбирать ту часть, рассматривать которую проще. Здесь на правой части всего одна нагрузка, поэтому рассмотрим равновесие правой
(от сечения) части балки (рис 10).
- Через т. С (центр тяжести поперечного сечения) проведены оси координат. Слева от сечения показаны возможные в плоской задаче внутренние силовые факторы (в положительном направлении). Уравнения равновесия представлены на рис 10.
- Для построения эпюр вычислим ВСФ на границах 3-го участка, подставив в (17), (18) крайние значения z3, т е 0 и 4м. Получим (19) - (22).
- Крайние точки для графика получены. Чтобы провести линии, нужно определить тип этих линий по ф. (17) и (18). Видим, что Q является константой, а M зависит от z3 линейно, поэтому на эпюре Q проводим горизонтальную прямую, а на эпюре M - наклонную прямую - между крайними точками. ( Механики откладывают отрицательные ординаты на эпюре моментов вниз, а строители - вверх. Эпюры на рис 6 построены для механиков.)
- Сечение с координатой z3 (рис 6) разбивает балку на 2 части - левую и правую. ВСФ можно определять из уравнений равновесия любой (по выбору) из этих частей. Рекомендуется выбирать ту часть, рассматривать которую проще. Здесь на правой части всего одна нагрузка, поэтому рассмотрим равновесие правой
(от сечения) части балки (рис 10).
- Освоив вышеизложенный подробный метод вычисления ВСФ, можно вычислять ВСФ более коротким способом, то есть сразу записывать выражение вида: ВСФ = ... . Например, формулу (6) в виде: Q = -YA можно записать сразу, если пользоваться таким правилом:
Поперечная сила Q в сечении равна сумме проекций всех внешних сил, действующих на рассматриваемую часть бруса на ось Y. Где ось Y - повернутая на 90o внешняя нормаль к сечению.
Аналогично: продольная сила N равна сумме проекций всех внешних сил, действующих на рассматриваемую часть бруса на внутреннюю нормаль к сечению.