

 Определение опорных реакций
Определение опорных реакций
- Если твердое тело находится в состоянии покоя (обычно в сопромате рассматривают такие конструкции) то приложенные к этому телу внешние силы взаимно уравновешены. При этом обязательно учитываются ВСЕ внешние силы, т е и заданная нагрузка и реакции опор; и сосредоточенные силы и моменты (пары сил) и распределенную нагрузку.
Примечание:
При решении задач сопротивления материалов собственным весом тела обычно пренебрегают.
- Следовательно, для системы внешних сил, приложенных к покоящемуся телу справедливы равенства:
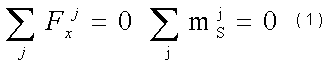 где: Fxj - проекция j-й внешней силы на ось X.
X - любая ось.
где: Fxj - проекция j-й внешней силы на ось X.
X - любая ось.
mSj - момент j-й внешней силы относительно точки S (для плоской схемы или относительно оси S - для пространственной схемы).
X, S - любая ось (любая точка).
Примечания:
- Проекция Fxj сосредоточенной силы Fj на ось X равна величине Fj (модулю вектора) этой силы умноженной на cos угла между векторами Fj и X. (Знак + - проекции определяется знаком cos).
- Перед суммированием распределенная нагрузка q заменяется равнодействующей Rq. Для равномерно распределенной нагрузки Rq = q*L, приложена в центре участка.
где L - длина участка равномерно распределенной нагрузки.
В общем случае равнодействующая распределенной нагрузки равна площади эпюры (графика) этой нагрузки и приложена в центре площади (тяжести) этой эпюры.
- Проекция пары сил на любую ось равна нулю (естественно, т к силы пары равны).
- Для плоской расчетной схемы:
- Пары сил и моменты сил считаются положительными, если действуют ПРОТИВ часовой стрелки.
- Момент пары сил относительно любой точки равен моменту этой пары (с учетом знака + -)
- Момент сосредоточенной силы относительно точки равен величине силы умноженной на плечо этой силы относительно точки. Плечо есть длина перпендикуляра, опущенного из точки на линию действия силы. Не забудьте определить знак + - момента.
- Так как осей и точек бесчисленное множество, то равенств (1) можно составить бесчисленное множество. В эти равенства входят неизвестные (реакции опор), поэтому их можно считать уравнениями и пытаться найти из них реакции опор.
- Из курса теоретической механики известно, что для пространственной системы сил существует 6 НЕЗАВИСИМЫХ уравнений статики (т е равновесия), а для плоской системы - 3. Поэтому для плоской расчетной схемы можно найти не более 3 опорных реакций, а для пространственной (3-х мерной) - не более 6. Остальные равенства типа (1) являются зависимыми и могут служить для проверки найденного решения.
- На практике для определения реакций опор выбирают такие уравнения равновесия, в каждое из которых входит не более 1 неизвестной реакции (если это удается). В строительной механике определяют так называемые МОМЕНТНЫЕ ТОЧКИ (точки, в которых пересекаются линии действия двух и более опорных реакций). Составляя уравнение равновесия в виде суммы моментов относительно моментной точки, мы избавляемся от нескольких "лишних" неизвестных.
Составляя уравнение равновесия: сумма моментов относительно шарнирной опоры мы получаем полезное уравнение, так как избавились от одного - двух неизвестных.






 Определение опорных реакций
Определение опорных реакцийгде: Fxj - проекция j-й внешней силы на ось X. X - любая ось.